Fantasy Cricket & Linear Programming
Published by Lakshmi E | Assistant Vice President, Client Solutions
- January 4, 2022
- Posted by: admin
- Category: Data Science


The Indian Premier League (IPL) is the biggest domestic cricket league on the globe and with the thirteenth edition underway, it is a perfect time to enjoy the game and explore some machine learning techniques along with it.
This year the IPL title sponsors are Dream11. Dream11 is a fantasy sports platform based out of India. It allows users to play fantasy cricket, hockey, football, kabaddi and basketball.
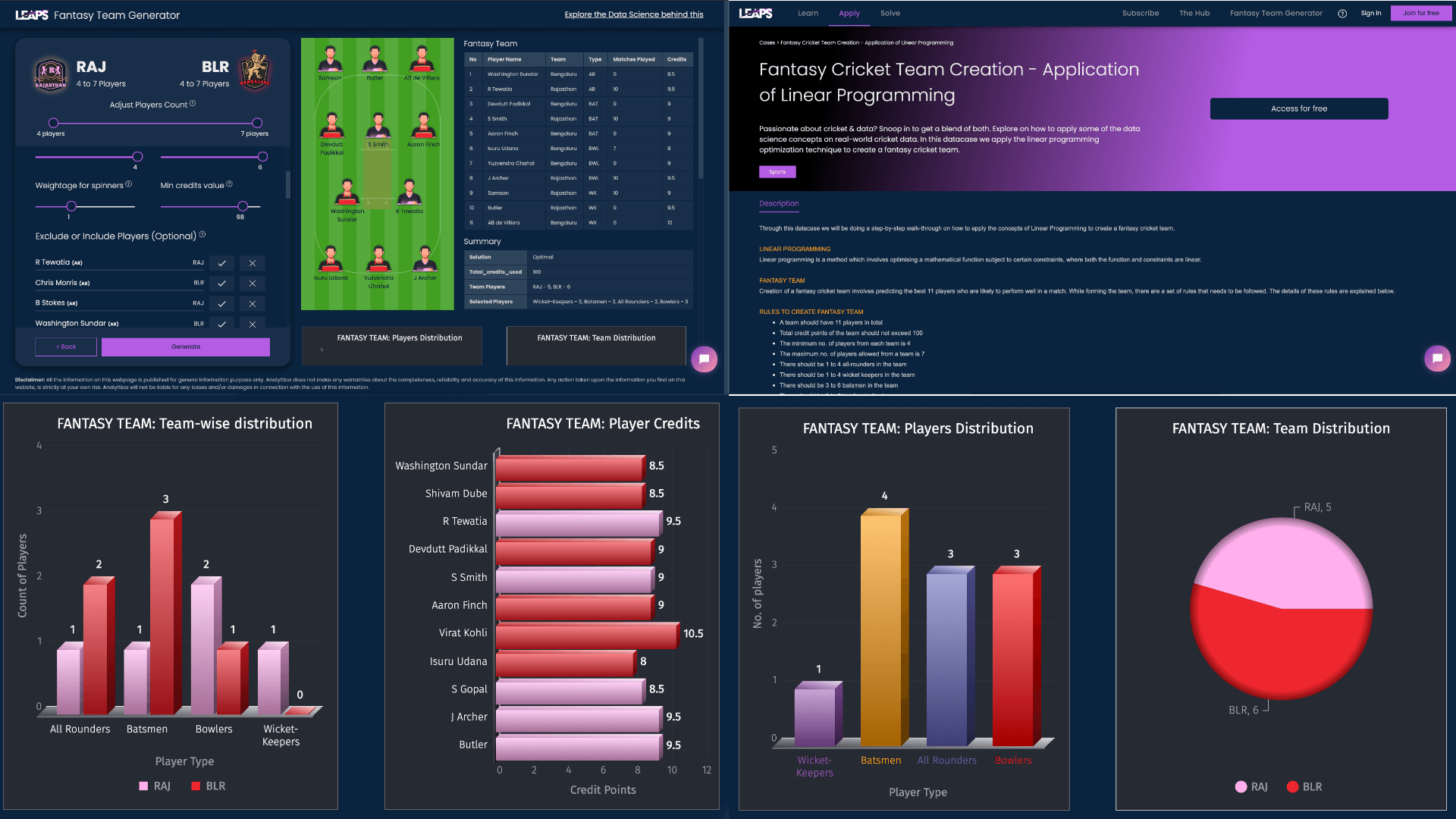

In this article we will be applying Prescriptive Analytics on sports where we will focus on selecting a fantasy cricket team with one of the matches as an example.
It will be a step-by-step code walk-through using Python. Along with it, we will also be using the open-platform Analyttica TreasureHunt® LEAPS to achieve the same without having to code.
Fantasy Cricket in a Nutshell
If you are new to fantasy cricket then this is how it works
- User needs to create a fantasy cricket team
- User can then participate in a contest with this team.
- Each player is assigned with a credit value. There is an upper limit on the total credit points in a team.
- Each player will fall into one of the following categories: batsman, wicket-keeper, bowler, all-rounder
- During the match, points are assigned to the players based on their performance & category.
- At the end of the match, based on the points, a team with the maximum points that adhere to all the rules will be the winning combination of best 11 players.
Rules to create a fantasy team
There are a set of rules that needs to be followed to build a team.
Following are the rules to form a fantasy cricket team
- A team should have 11 players to total
- There should be 1 to 3 all-rounders in the team
- There should be 1 to 3 wicket keepers in the team
- There should be 3 to 6 batsmen in the team
- There should be 3 to 6 bowlers in the team
- Total credit points of the team should not exceed 100
- The minimum no. of players allowed from each team is 4
- The maximum no. of players allowed from each team is 7
How to pick the players
Additionally, for every match, following information is available for each of the players:
- Points made by the player in the previous matches of the same tournament
- Average points per match for a player
- of times the player has been in the best11 team in the past matches of the same tournament
- Percentage of times the player has been in the best11 team in the past
Any of the above metrics can be used to pick the best team.
Linear Programming
Linear Programming in Operations Research is one of the scientific techniques that is used to get an optimum solution to the given business problem by taking resource scarcity and constraints into account.
Linear programming allows us to model real-life problems into mathematical models represented by linear relationships. It involves an objective function to define what we are trying to achieve and the creation of constraints as linear inequalities. As the name clearly specifies, the relationship between the objective function and constraints should be linear in nature (one-degree equations).
Relationship between Fantasy Cricket & Linear Programming
Linear programming can be used to solve many real-life problems and fantasy cricket is one of them.
In order to create a fantasy team one needs to select the best players based on a objective. The final team formed should follow all the rules or constraints put by the platform.
This makes it a perfect problem that can be solved with Linear Programming. We need to maximize the team’s selection metric projection, while respecting the given budget (credits) and team composition constraints.
Approaches to build the solution
Here we will be using two approaches to build the solution, one for users who wish to code & solve and the other is dedicated to users who want to learn the concept and apply it using the tools.
We will go through both the approaches here:
Approach 1: Solving the Linear Problem using the Python package PuLP
Approach 2: Solving the Linear Problem using Point & Click functions on ATH LEAPS
Feel free to try out any of the approach that excites you.
Getting started with ATH LEAPS
Analyttica TreasureHunt® LEAPS is a patented open-platform to Learn, Apply & Solve all the machine learning and AI problems of a data analyst/scientist. It has over 650 inbuilt functions that can be leveraged through simple point & click. It also provides a coding console for those wanting to get their hands dirty.
You can refer to this datacase on LEAPS: https://leaps.analyttica.com/sample_cases/2273
In this case study we will go through both the approaches to solve the problem.
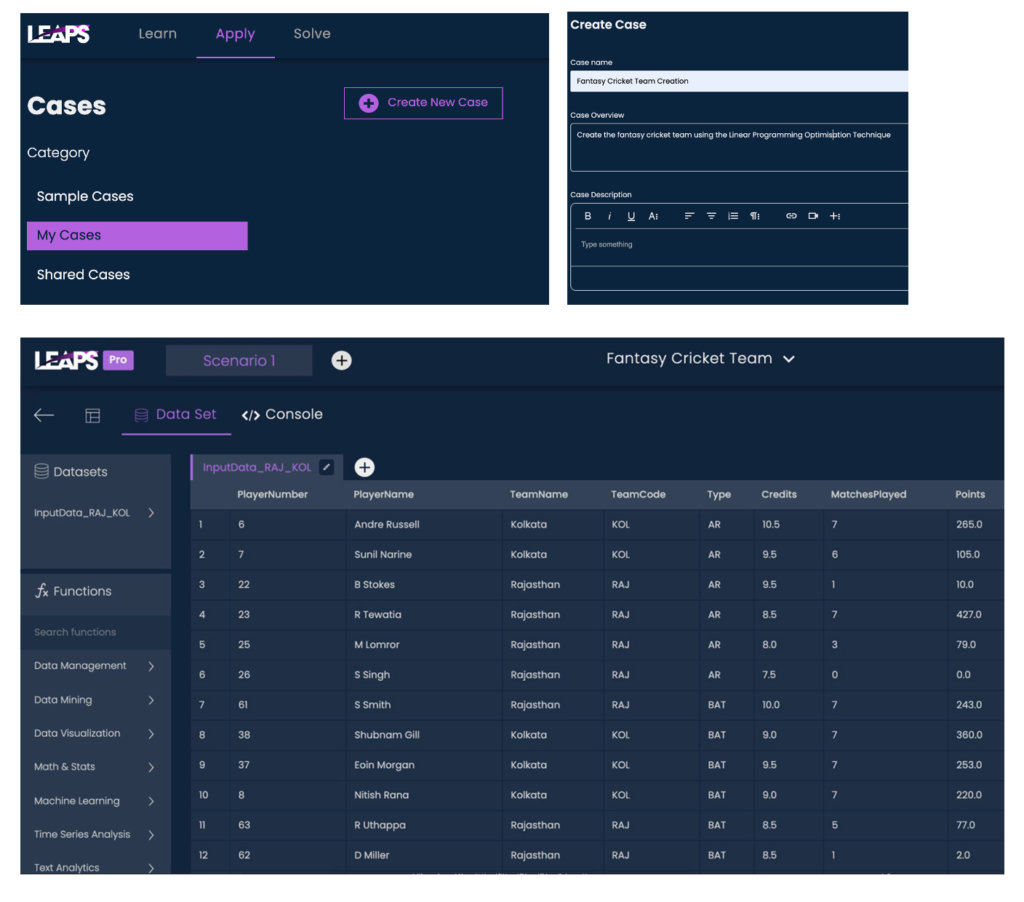
Register yourself at https://leaps.analyttica.com
Choose the “Apply” section on the top left of the screen. Choose “My Cases” – “Create New Case”. Provide the case name, description, dataset and you are good to get started.

NOTE: Approach 1 can also be done on any Python IDE but might include the additional overhead of setting up the dependent packages like pulp & ipywidgets.
Approach 1: Solving the Linear Problem in Python using PuLP
We will be using the python package PuLP to create the linear problem and solve it.
In addition to the provided rules, additional constraints can be added for the users to play around and create the best suited team.
Once an optimal solution is identified, it will generate the fantasy team along with some summary details. In addition, we will also be using the ipywidgets package to build an UI in Jupyter notebbok for users to input the additional constraints.
The code snippets below is a part of the complete code to help the readers understand & try out the flow.
Approach 1: Get started with ATH LEAPS
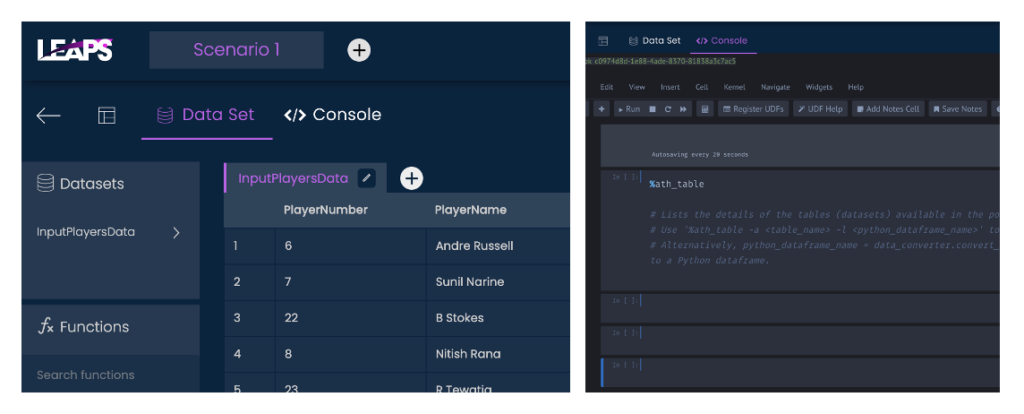
If you are trying this out on ATH LEAPS, then choose the console option on the top to start a jupyter kernel

Approach 1: Package installations
In addition to the regular packages like numpy, pandas, sklearn, this code also requires the installation of pulp.
In case you are using pip, all the packages can be installed with the ‘pip install’ command.
NOTE: This step is not required if you are working on ATH LEAPS.
Approach 1: Input Data
The program will require two kinds of input. One will be the player details and other will be the user configurations to building the linear problem.
The player details is provided in a csv file. Sample contents of the file will be like below.


Approach 1: Create the Linear Programming problem
Create the linear programming problem with a name


Approach 1: Create the variables
Prepare the variables required to create the objective function and the constraints.
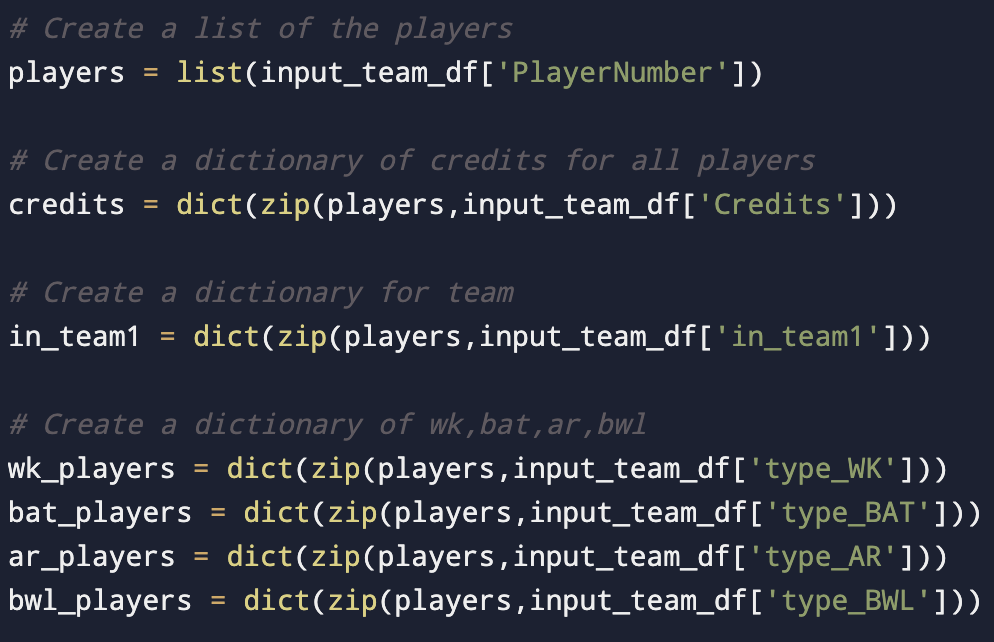

Similar variables should be created for each of the constraints. Shown above is a sample. Same approach can be used to create all the required variables.
Approach 1: Defining the objective function
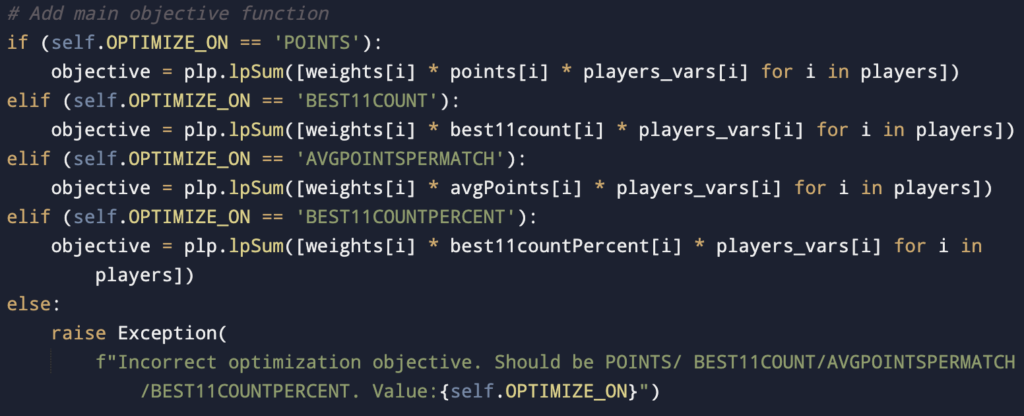
Here the objective function could be defined based on one of the below:
- Maximize based on each player’s points
- Maximize based on no. of times the player has been in the best11 team in the past
- Maximize based on average points per match
- Maximize based on percentage times player is been in best11 team
This choice can be given to the user to configure based on which the objective function can be set.

Approach 1: Adding the constraints
Constraint based on number of players
There should be exactly 11 players in the final team. This can be set with the below constraint.


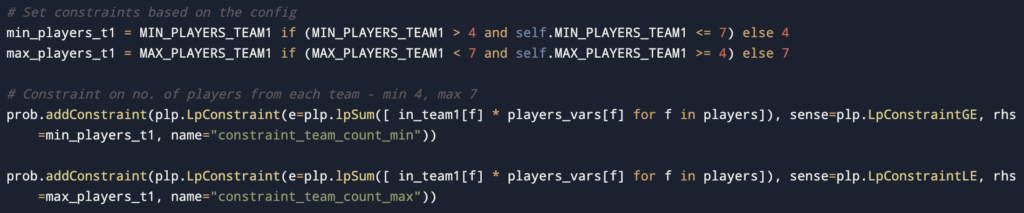
Constraint based on players from Team 1
Each team can have 4 to 7 players. This can be configured further by the user if required.

Constraint based on players in the line-up
Since the playing 11 will be known only during the toss (normally 30 minutes before the start of the match), a constraint can be added on the players to be picked.
- Select from all players (default)
- Select only players who have played the last match
- Select only players who have played atleast one match
- Select only players who are in the playing 11 of that match


Above are some samples on how the constraints can be set. Similarly, all the required constraints can be set.
Approach 1: Ready to solve?
Now that the constraints are added and the objective defined, we are ready to solve the problem.
Since the goal is to maximize the objective, set the objective details to the problem accordingly and allow pulp to solve it.


Approach 1: Intepreting the results
Linear program will try to solve the problem by identifying the best selection that will maximize the objective function and also fulfilling all the constraints that have been set.
In case it is not able to find any feasible solution with the given constraints, then it will return the status as infeasible. Pulp will drop the constraints that cannot be fulfilled and return an output.


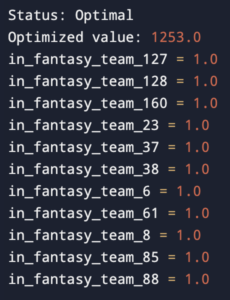
Sample output

Approach 1: Playing around with the data
To make the application more interactive, ipywidgets have been used so that the configuration values can be selected by the user on a Jupyter notebook.
We will not go through the details of creating the widgets on Jupyter notebook as a good amount of documentation is already available for it and also it is not our area of focus here.
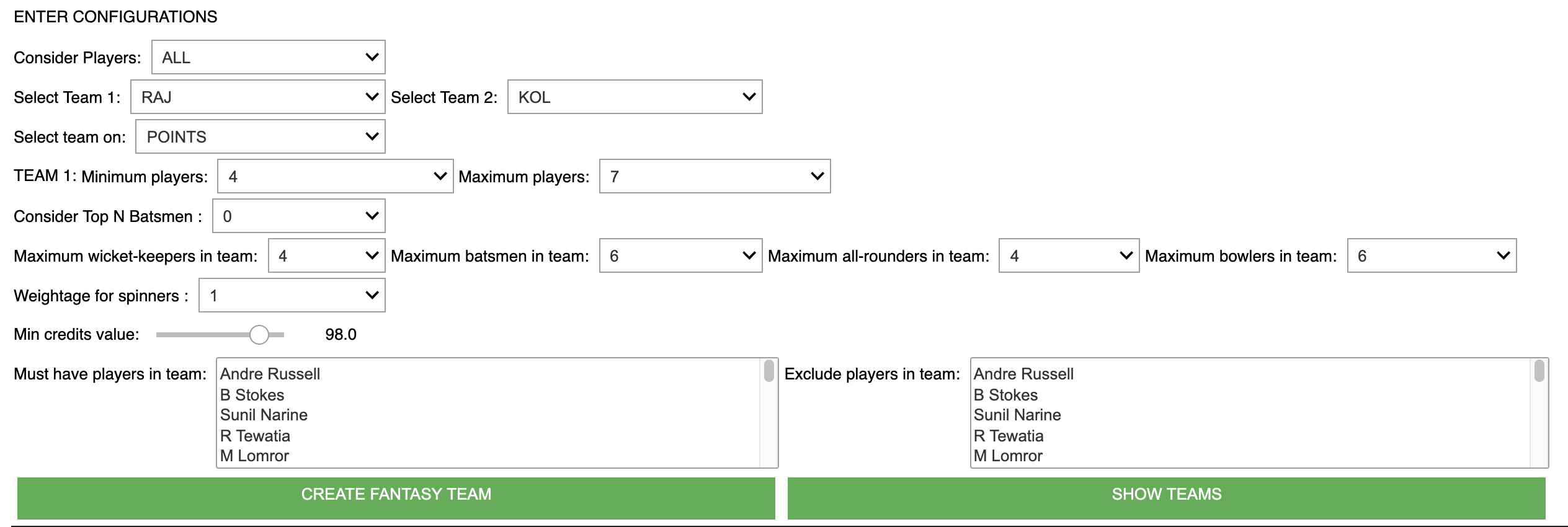

These configurations are internally converted to either the objective function or constraints.
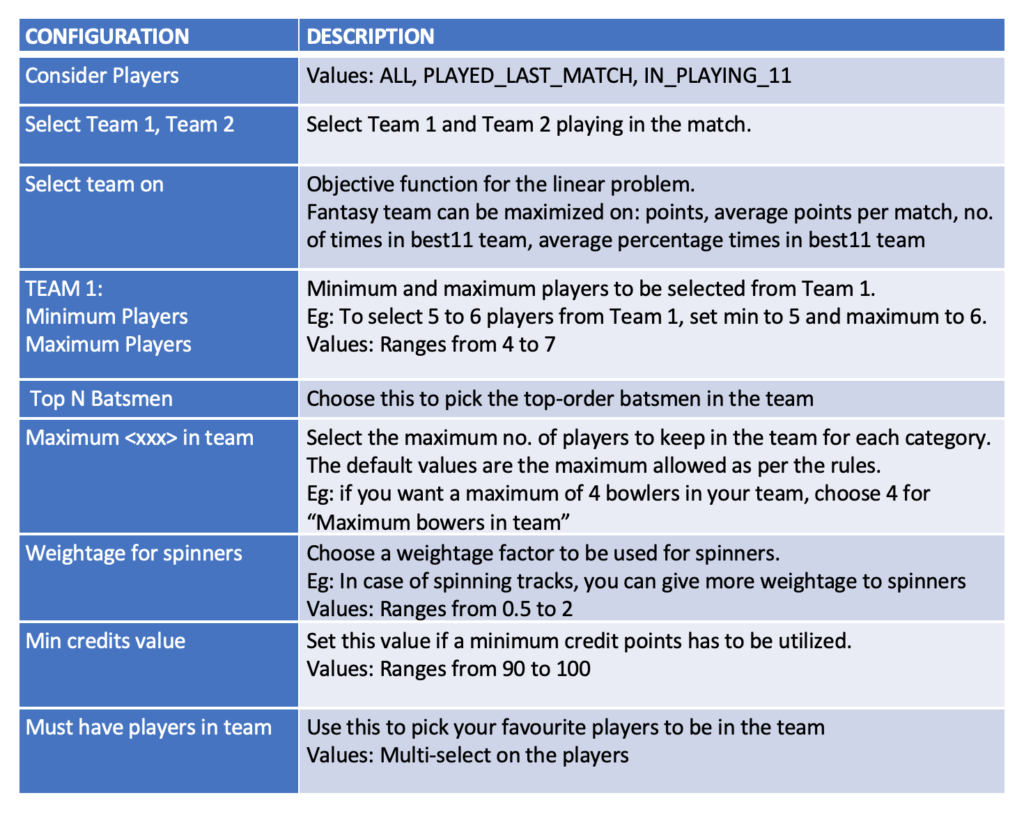

Approach 1: Configuring and creating a team – Sample Result
Give your choice of constraints and click on the “CREATE FANTASY TEAM” button.


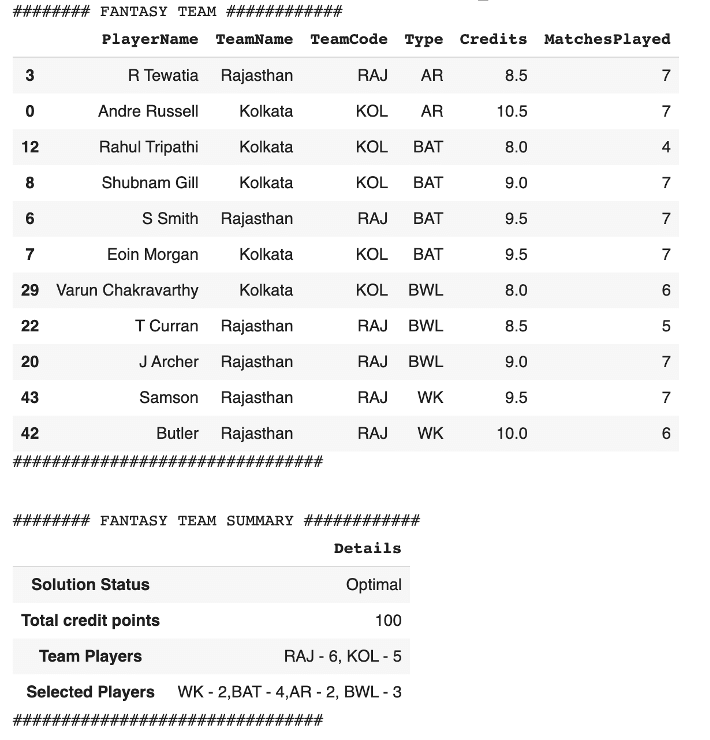

BANG!!! You are ready with your fantasy team to start participating in the contests!!
Approach 2: Solve using the Point & Click functions on ATH LEAPS
In this approach we will see how this problem can be solved without having to code. Here we will be using the point and click functions that are readily available on the platform.
To solve this problem, we first need to convert the data to the required format that can be fed into the Linear Program
Approach 2: Prepare the data to be fed into the Linear Program
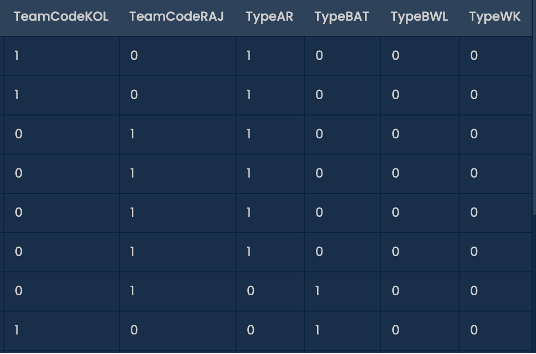
Step 1: “Dummy Variable” – One-Hot Encoding
Create dummy variables from the categorical variables so that constraints can be applied on them.
Note that the categorical variables are created twice as two constraints need to be applied on each of the categories for the lower limit and the upper limit.

Step 2: “Rename Columns” (optional)
Rename columns to match the constraint name. This is an optional step.

Step 3: “Transpose”
Transpose the columns so that each constraint variable is available as a row in the table. The player name will be column headers as the final result should be a binary flag on each player to indicate if they are in the team or not.
Input to Transpose Function:


Output of Transpose Function:
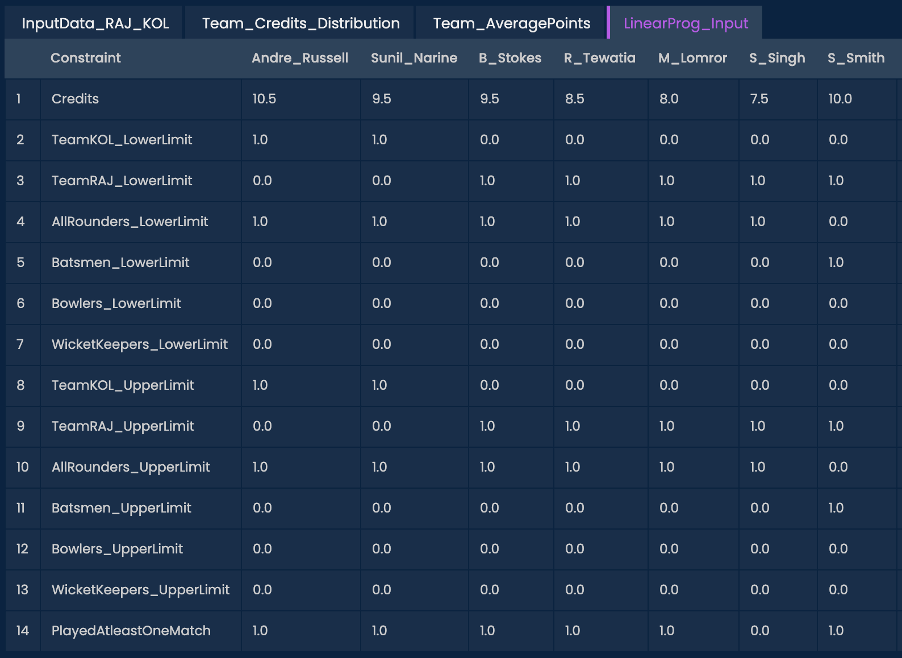

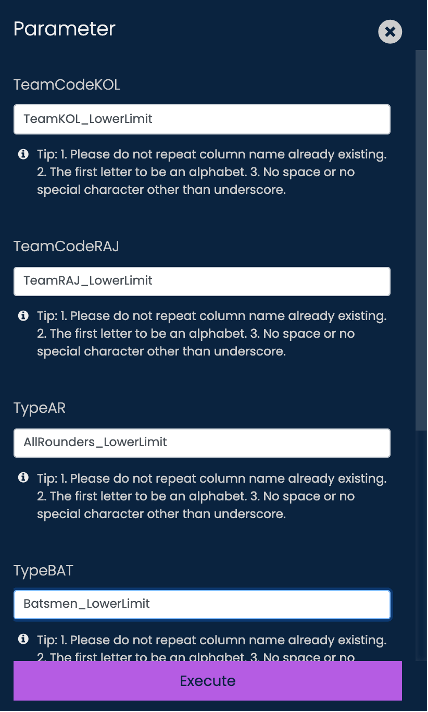
Step 4: “Alias”
Run the alias function to create the columns for the constraint condition and the decision variable.
The constraint condition will be the inequality conditions like “<=”,”=”,”>=”
The decision variable will be the values that will decide the output. It is essentially the right-hand side of the inequality equation.
Eg: For setting a constraint on total credits to be within 100, following should be set:
ConstraintName: “Credits”, Condition: “<=”, Decision Variable: “100”
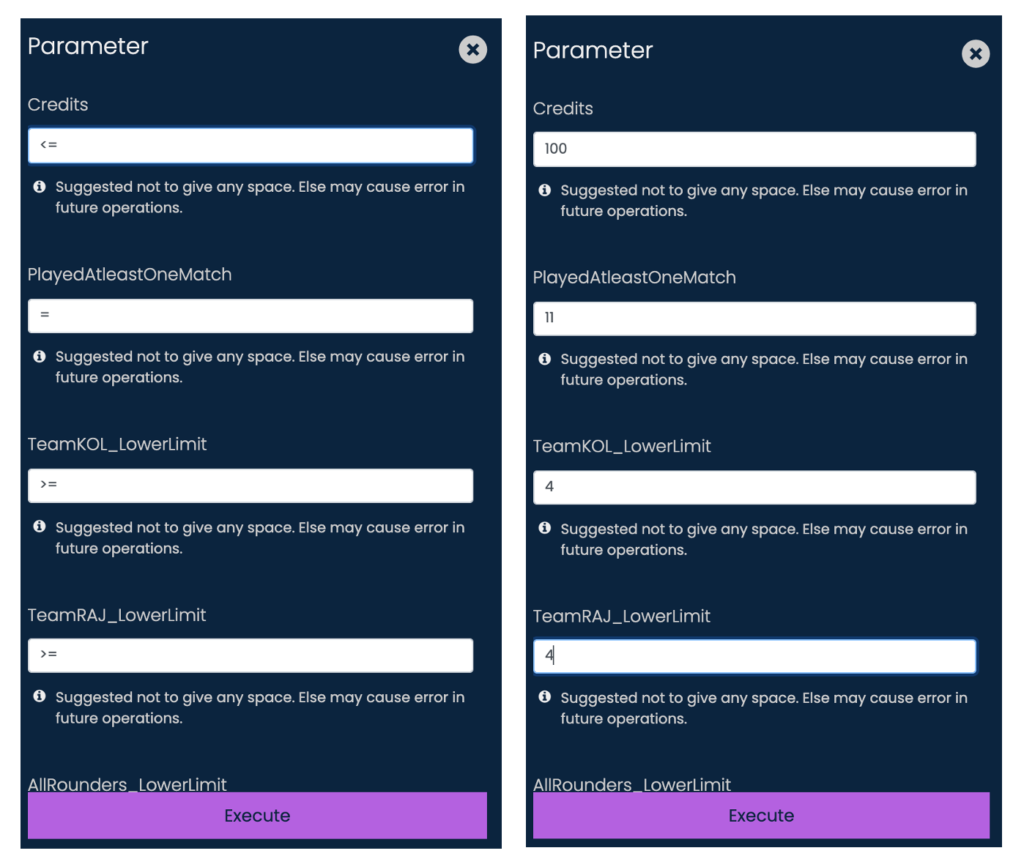

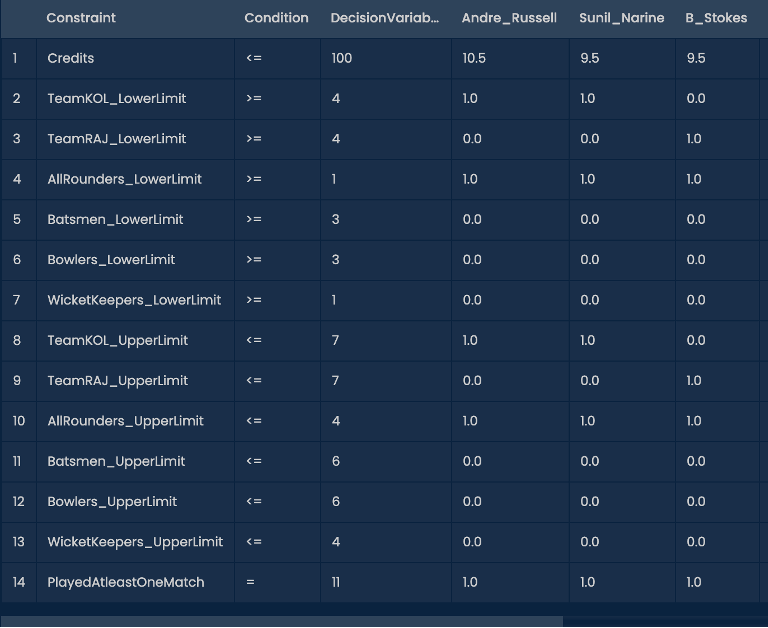
Step 5: “Rename Columns” (optional)
Change the name of the new columns created by alias to match the terminologies in Linear Programming.
This is an optional step and will not impact the output in any way.


Summary after data preparation
The above 5 steps will convert the input data to a format that can be directly fed into the linear programming function to give us the fantasy team.

Approach 2: Solve the problem
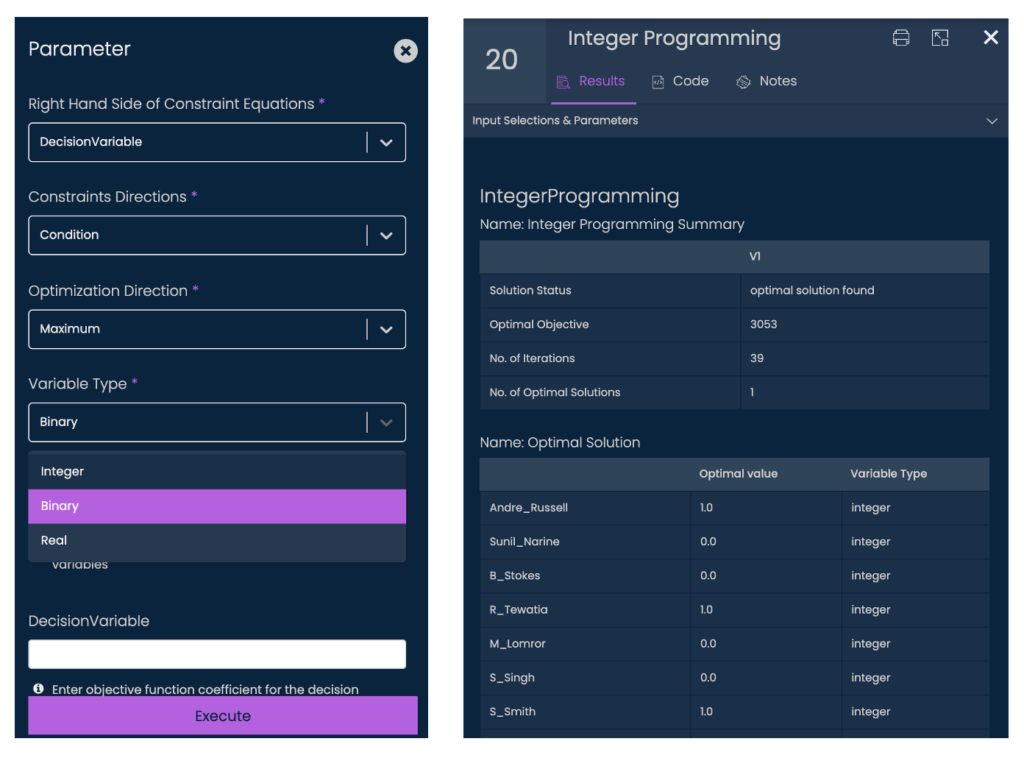
Step 6: “Integer Programming”
Run the Integer Programming function with the required parameters to get the solution.
Variable type has to be set to Binary in this case as we want to have a binary output on whether the player should be in the fantasy team or not.
If the solution cannot be found with the given constraints, then the function will return the result as infeasible solution. If a solution is found, then the result will be “optimal”.
In the solution identified below, the optimal flag will be set to 1 for the 11 players who should be included in the fantasy team. It has found the maximum player points as 1253 with the given constraints. Here 14 constraints have been used. Similarly, more constraints can be added.

hat’s it!!! 6 simple steps to be followed and you are ready with the fantasy team without having to write a line of code.
Conclusion
This article is a simple example of how we can apply the linear optimization technique on cricket to pick the best players. The principles of linear optimization can be applied to many problems that have a fundamentally simple goal like scoring more fantasy points or being a popularly selected player.
Try it out and play with it. To explore more, we can get in some more historical data for each of the players and add that to the selection constraints. Though this may not make the elite team always, it will surely guide the user while picking the team.
Check out the sample cases section in LEAPS for this datacase with all the steps for further reference.
Disclaimer: the fantasy team is only suggestive based on the data provided and the constraints given. It is not guaranteed that these players will be in the best11 team at the end of the match. Please use your own judgment while picking the team 😉.
